Stress Strain Calculation of a Laminate#
This example presents the stress strain calculation of a Laminate using the CLT.
[17]:
import matplotlib.pyplot as plt
import pandas as pd
from composipy import OrthotropicMaterial, LaminateProperty, LaminateStrength
[10]:
# Material
E1 = 137.9e3
E2 = 11.7e3
v12 = 0.31
G12 = 4.82e3
t = 0.1524
#Loads
Nxx = 100
Mxx = 20
# Quasi laminate
stacking = [45, -45, 90, 0]
stacking += stacking[::-1]
# Object definition
material = OrthotropicMaterial(E1, E2, v12, G12, t)
laminate = LaminateProperty(stacking, material)
strength_analysis = LaminateStrength(laminate, Nxx=Nxx, Mxx=Mxx)
Calculating strains at the midplane \(\varepsilon_{0x}\), \(\varepsilon_{0y}\) and \(\gamma_{0xy}\)
[11]:
strength_analysis.epsilon0()
[11]:
array([ 1.52630215e-03, -4.89003289e-04, -1.67758599e-20, 5.46178270e-03,
-2.99304212e-03, -6.90268796e-04])
Calculating strains ply by ply in analysis direction and material direction.
[15]:
df_strain = strength_analysis.calculate_strain()
df_strain.head(6) #display the first 6
[15]:
| ply | position | angle | epsilonx | epsilony | gammaxy | epsilon1 | epsilon2 | gamma12 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | top | 45 | 4.86e-03 | -2.31e-03 | -4.21e-04 | 1.06e-03 | 1.48e-03 | -7.17e-03 |
| 1 | 1 | bot | 45 | 4.02e-03 | -1.86e-03 | -3.16e-04 | 9.25e-04 | 1.24e-03 | -5.88e-03 |
| 2 | 2 | top | -45 | 4.02e-03 | -1.86e-03 | -3.16e-04 | 1.24e-03 | 9.25e-04 | 5.88e-03 |
| 3 | 2 | bot | -45 | 3.19e-03 | -1.40e-03 | -2.10e-04 | 1.00e-03 | 7.90e-04 | 4.59e-03 |
| 4 | 3 | top | 90 | 3.19e-03 | -1.40e-03 | -2.10e-04 | -1.40e-03 | 3.19e-03 | 2.10e-04 |
| 5 | 3 | bot | 90 | 2.36e-03 | -9.45e-04 | -1.05e-04 | -9.45e-04 | 2.36e-03 | 1.05e-04 |
Note#
The sequence of the DataFrame starts from the TOP OF THE LAYUP to the BOTTOM OF THE LAYUP, which is the reverse of the definition order. When defining the laminate, the first element of the list corresponds to the bottom-most layer. This is especially important for non-symmetric laminates.
[27]:
df_strain_top = df_strain[df_strain['position']=='top'] #filter the top position
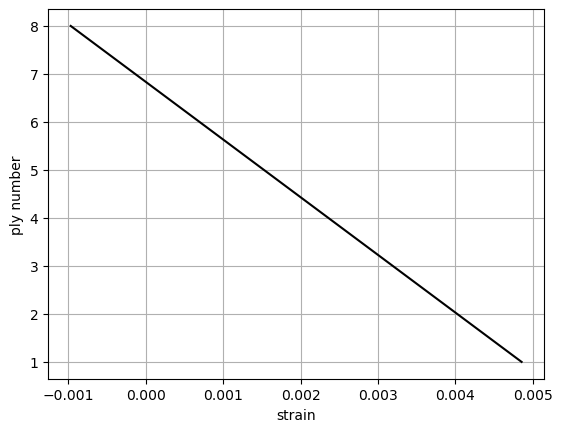
plt.grid()
plt.xlabel('strain')
plt.ylabel('ply number')
plt.plot(df_strain_top['epsilonx'], df_strain_top['ply'], 'k')
[27]:
[<matplotlib.lines.Line2D at 0x1dee71542e0>]
Calculating stresses ply by ply in analysis direction and material direction.
[16]:
df_stress = strength_analysis.calculate_stress()
df_stress.head(6) #display the first 6
[16]:
| ply | position | angle | sigmax | sigmay | tauxy | sigma1 | sigma2 | tau12 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | top | 45 | 121.68 | 52.57 | 65.77 | 152.89 | 21.36 | -34.56 |
| 1 | 1 | bot | 45 | 103.94 | 47.25 | 57.58 | 133.17 | 18.02 | -28.35 |
| 2 | 2 | top | -45 | 124.02 | 67.33 | -80.22 | 175.90 | 15.45 | 28.35 |
| 3 | 2 | bot | -45 | 99.59 | 55.32 | -64.48 | 141.93 | 12.97 | 22.14 |
| 4 | 3 | top | 90 | 32.52 | -183.16 | -1.01 | -183.16 | 32.52 | 1.01 |
| 5 | 3 | bot | 90 | 24.37 | -122.78 | -0.51 | -122.78 | 24.37 | 0.51 |
Note#
The sequence of the DataFrame starts from the TOP OF THE LAYUP to the BOTTOM OF THE LAYUP, which is the reverse of the definition order. When defining the laminate, the first element of the list corresponds to the bottom-most layer. This is especially important for non-symmetric laminates.
[30]:
df_stress_top = df_stress[df_stress['position']=='top'] #filter the top position
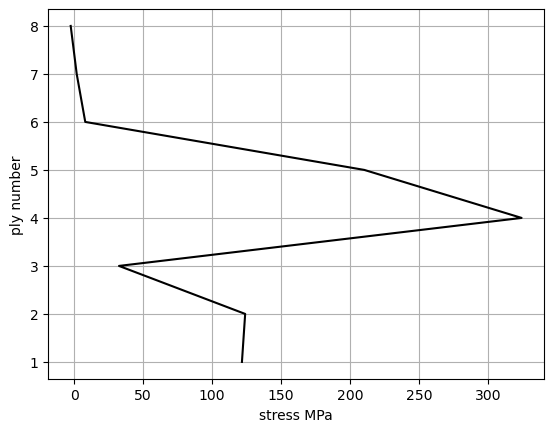
plt.grid()
plt.xlabel('stress MPa')
plt.ylabel('ply number')
plt.plot(df_stress_top['sigmax'], df_stress_top['ply'], 'k')
[30]:
[<matplotlib.lines.Line2D at 0x1dee72b1790>]
